EXAMPLE 1
A steam plant manager is proposing to upgrade a section of pipe shown below from E-3 to P-2. To save on material costs, he wants to install the smallest available size while keeping the steam velocity at P-2 to 6 ft/s minimum. The compressor outputs a steady flow of 100 lbm/hr superheated vapor steam at point P-1 to a pressure of 200 psia at 400 F. The steam flows through an isentropic turbine and insulated pipe network to point P-2 per the following diagram:
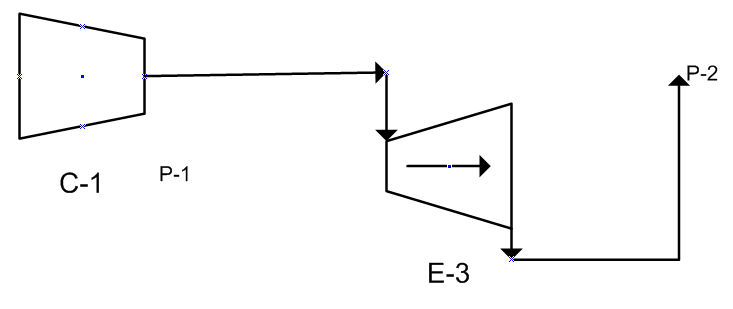
The isentropic turbine releases the steam vapor at atmospheric pressure. The pipe from P-1 to E-3 is schedule 40-5 in pipe. The plant manager is proposing a schedule 40- 4 inch welded, seamless steel pipe. Is the pipe size sufficient?
SOLUTION:
At first glance there looks to be a lot going on in this problem, but really this is a relatively straight forward 1st law problem with a few simplifications we can take advantage of.
We’re after the actual steam velocity at point P-2. We can equate velocity to terms we are given in the problem statement. Noting that velocity through a pipe [ft/hr] is the volumetric flow [ft3/hr] divided by the area [ft2] of pipe:
And the volumetric flow [ft3/hr] is the mass flow [lbm/hr] multiplied by the specific volume [ft3/lbm],
Gives us:
The plant manager is proposing a schedule 40- 4 inch pipe so we can calculate A. Mass flow is given as well. But we need to know the specific volume (ν) to proceed.
Finding ν:
We need to know two properties at a given point in order to completely define a system.
Two Property Rule: The state of a substance may be defined by any two independent properties, and all other properties may be found if two independent properties are known.
The discharge pressure of the turbine (and therefore point P-2) is given as atmospheric pressure (14.7 psia). Per the two property rule, we need one more property to fully define the system and be able to determine the specific volume.
The conditions out of the turbine are given as atmospheric pressure. However we know that the process across the turbine is isentropic, therefore si=so. Since two properties are known upstream of the turbine (200 psia and 400 F), we can read si directly from the superheated tables as si=1.5602 Btu/(lbm-R). This is identical to the entropy out of the turbine, so. We now have two properties for P-2, 14.7 psia pressure and entropy of 1.5602 Btu/(lbm-R). From here the value of νo can either be read from tables or a pressure-enthalpy diagram. There are pros and cons for both reading values from tables and using a pressure enthalpy diagram. I will find the value of νo both ways to illustrate this.
METHOD 1: Calculation and tables
The steam coming out of the turbine is not necessarily saturated so we need to calculate it’s quality (x) before determining the exact specific volume. We know the value of so so we will use that as a starting point:
At atmospheric conditions, sf and sfg are 0.3122 Btu/(lbm-R) and 1.4445 Btu/(lbm-R) respectively. Therefore substituting into the quality equation gives:
And x=0.8639. We can use the quality equation again to calculate νo. Note if your using the steam tables from the MERM, the specific volume values are only given in νf and νg (not νfg therefore the second form of the quality equation must be used:
From the saturated steam tables ν f and ν g are 0.01671 ft3/lbm and 26.80 ft3/lbm respectively.
from this we find νo=23.15 ft3/lbm.
METHOD 1: enthalpy diagram:
Your known values are pressure (atmospheric) and entropy s=1.5602 Btu/(lbm-R). Take a look at a typical pressure-enthalpy diagram for steam below:
The green lines represent entropy and the orange horizontal line (temperature=212F) is the atmospheric pressure across the mixed quality boundary. Most of the entropy lines don’t extend into the mixed quality area but you can take a pencil and lightly trace where the s=1.56 Btu/(lbm-R) line would extend down like this:
The solid green line between s=1.40 and s=1.60 extends down to the atmospheric pressure line. Note how the purple density lines move across the mixed quality portion of the graph. Tracing the ρ=0.04 lb/ft3 line across this boundary, we can see that the point where our known values of s=1.56 Btu/(lbm-R) and 14.7 psia intersect is about ρ=.045 lb/ft3. The reciprocal of density is specific volume:
This gives us νo=1/.045=22.2 ft3/lbm is within a few percent of the calculated value of 23.15 ft3/lbm and only takes a few seconds to do.
PE exam strategy: Using gas diagrams can often save valuable time on the test as values can be read directly for any state with minimal to no calculations required. Be sure to be comfortable using both tables and diagrams.
Revisiting our initial equation to solve,
Shows that we only need to calculate A to check whether the velocity of the steam with schedule 40- 4 inch pipe is acceptable.
CALCULATION OF Ao:
From the problem statement:
The pipe from E-3 to P-2 is schedule 40-4 in pipe.
Several common PE exam references will have information on pipe diameters for schedule 40, 80, 120, etc. diameter pipe. Of course your Mechanical Engineering Reference Manual (MERM) has a section on this in their appendix as well as the Marks’ Standard Handbook for Mechanical Engineers which is also recommended and very popular. A schedule 40, 4” diameter pipe has an internal diameter of 4.026 inches. The wording in the problem gives a specific pipe type (seamless steel pipe) which suggests you should use the exact dimension as given in your tables for this type and size of pipe, however here is a good example of an opportunity to use some common sense and save valuable time on the exam. The numerical difference between the actual diameter of 4.026 inches and the nominal diameter of 4.0 inches is very small. This difference will end up making very little difference in the final result. Unless the available answer choices are all very close numerically, it may not be worth the time to look up the actual exact diameter.
PE exam strategy: Examine the available answers to choose from given with each problem statement. Unless the available answers are all very close together numerically, it may save valuable time to assume nominal pipe diameters when a specific pipe schedule diameter is given.
For this exercise we will use the exact value of Di=4.026”
We now have all the values we need to calculate the final result. Going back the required form of our original equation we have:
Therefore, the minimum required steam velocity is 6 ft/sec so a pipe size of 4” nominal is sufficient
